CONCEPTOS BÁSICOS DE LA ESTADÍSTICA.

Población:conjunto de elementos con unas características similares sobre el cual se pretende hacer un estudio estadístico.

Muestra:parte de la población sobre la cual se realiza el estudio estadístico.

Individuo: cada uno de los elementos que forman parte de la población.
Carácter: cada una de las características que poseen todos los individuos de una población y que, por tanto, puede ser objeto de un estudio estadístico.

Muestreo: proceso por el que se selecciona la muestra de una población. Existen diferentes métodos de muestreo.
Variable estadística: característica de los individuos de una población que puede adoptar diferentes valores y puede medirse. Suele ser la característica que se estudia en una investigación estadística.

TABLA DE FRECUENCIA.

La tabla de frecuencia se divide en marca de clase y 4 frecuencias.

Marca de clase (xi).
Frecuencia absoluta (f).
Frecuencia acumulada (fa).
Frecuencia retaltiva (fr.).
Frecuencia porcentual (fr%).

En primera fila, que es la marca de clase (xi) pondremos los datos ordenados de menor a mayor.

En la segunda fila que es la de frecuencia absoluta (f), será de poner la cantidad de las veces que está repetido el número.

En la tercera fila que es la frecuencia acumulada (fa) sumaremos las frecuencias absolutas y lo vamos poniendo en la fila de la frecuencia acumulada y su fórmula es:

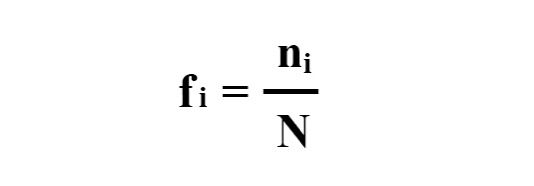
En la cuarta fila, que es la frecuencia relativa (fr.) dividiremos la frecuencia absoluta por el número tatal de datos que son 40 y su fórmula es:

En la quinta fila, que es la de frecuencia de porcentaje (fr%) multiplicaremos la frecuencia relativa x 100 y el resultado será la la frecuencia porcentual.

GRAFICA. Aquí se muestran los resultados obtenidos de la tabla de frecuencias.

CLASIFICACIÓN DE VARIABLES.

En estadística existen dos tipos de variables, cuantitativas y cualitativas.

Las cuantitativas son aquellas las que cuyo resultado es un número.
Las cualitativas son aquellas cuyos resultados posibles no son numéricos.

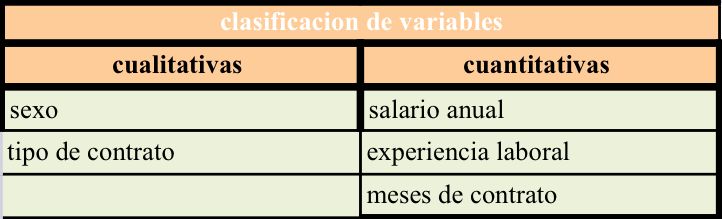
En este caso las cualitativas son: sexo y tipo de contatro porque cuyos resultados no son numéricos.

En las cuantitativas son: Salario anual, Experiencia laboral y meses de contratos porque cuyos resultados son numéricos.

MEDIDAS DE TENDENCIA CENTRAL.

Las medidas de tencendia central son los parametros mas utiles ya que ubican el valor de un conjunto de datos, las medidas de tencendia central mas comunes son las siguientes:

Moda
Media
Mediana

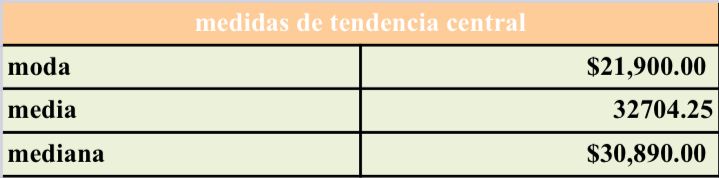
En la tabla aparecen las medidas de tendencia central.

La moda es el número que mas veces aparece en la trabla de frecuencias, que en este caso es el $21,900.00.

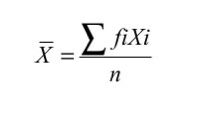
En la media tenemos que sumar todos los valores y dividirlos por la cantidad de el número total de datos y su fórmula es la siguiente.

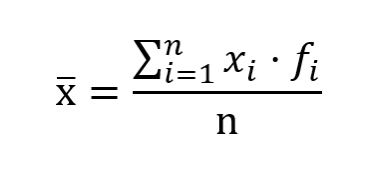
En la mediana tenemos que ordenar los datos de menor a mayor y elegir el número que se encuentre en la mitad de todos los datos y esa sería la mediana, su fórmula es la siguiente.

INTERPRETACIÓN DE DATOS.

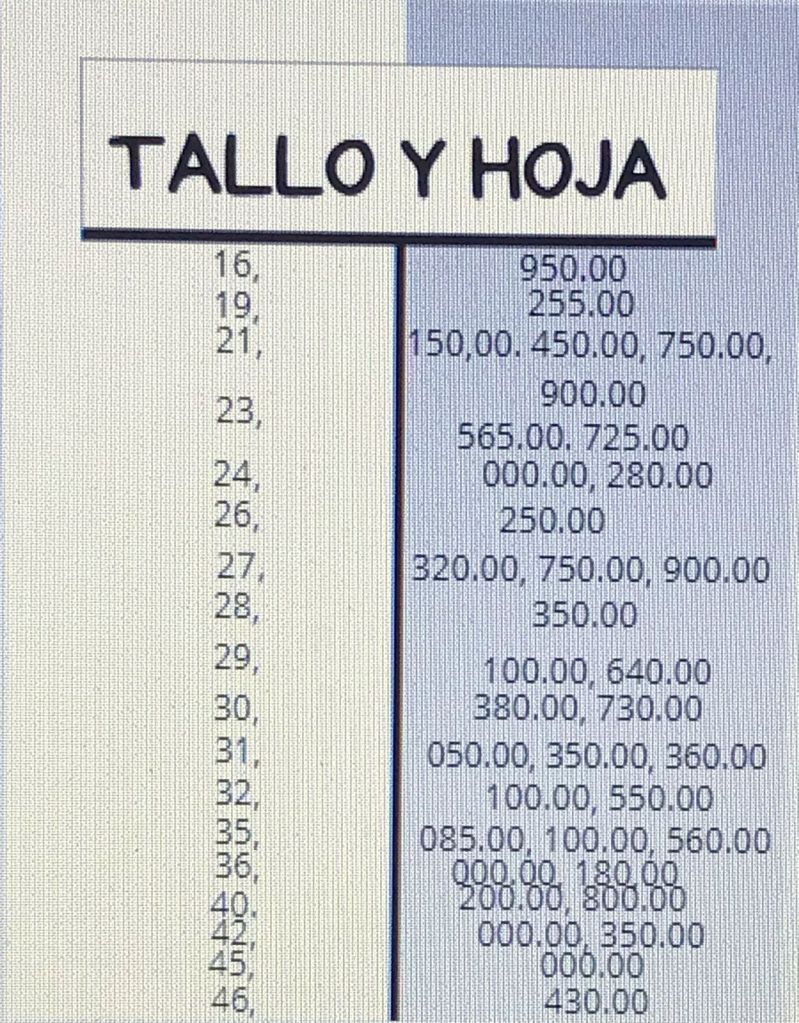
DIAGRAMA DE TALLO Y HOJA.

El diagrama de tallo y hoja es util para conjuntos de datos de tamaño medio es decir entre 20 y 50 elementos con este semidiagrama podemos darnos cuenta de la asimetría de los datos.

CONSTRUCCIÓN DE UN DIAGRAMA DE TALLO Y HOJA.

Ordenar los datos
Dibujar una tabla con dos columnas, la primera columna sera el tallo y la segunda la hoja.

MEDIDAS DE POSICIÓN.

Cuantil: es una medida de posición que se utliza para descubir propiedades de un conjunto de datos numéricos loscuantiles mas comunes son: Cuantil, decil y persentil
Cuantil: Son los valores numéricos que dividen a la muestraya ordenada en 4 partes iguales,
El primer cuantil tiene un valor de 25% de las observaciones son menores y el 45% son mayores.
El segundo cuantil tiene un valor de 50% de las observaciones son mayores y el resto son menores.
El tercer cuantil tiene un valor de 75% de las observaciones son menores y el 25% son mayores.

Q1= 40+1/4=10.2 =24,80.00+26,250.00/2=14,365

Fórmula del cuantil 1. ( n+1)/4

Q2= 31,050.00. 50/100=0.5 x 40=20

Q3=38,850.00. 75/100=0.7 x 40=30

Fórmula del cuantil 2 y 3, (p/100) x n.

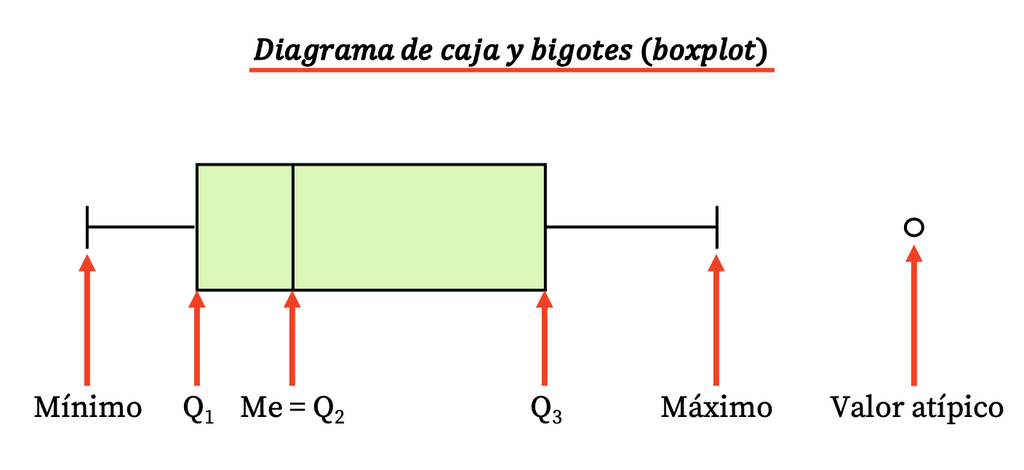
DIAGRAMA DE CAJA Y BIGOTE

La principal característica del diagrama de caja y bigotes es que permite visualizar rápidamente la dispersión de una serie de datos, ya que indica los cuartiles, la mediana, los valores extremos y los valores atípicos de los datos.